|
Beim Wankelmotor beträgt die Taktdauer 270° Exzenterwellendrehung, im Gegensatz hierzu dauert bei einen Hubkolbenmotor ein Takt nur 180° Kurbelwellendrehung. So ergibt sich für jede Exzenterwellenumdrehung ein
Arbeitstakt pro Kammer. Ein komplettes Arbeitsspiel beträgt beim Wankelmotor 1080°. Um vergleichbar mit einen 4T-HKM zu sein, kann ein imaginäres Vh genutzt werden. Hintergrund ist der wegen dem Leertakt beim
4T-HKM nur halb so große Füllungsdurchsatz, im Vergleich zum Wankelmotor.
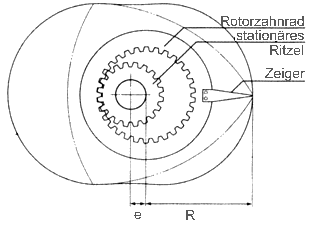
Vk = 5,19615*(R+a)*e*B R = erzeugender Radius a=Äquidistante e = die Exzentrizität B=Kammerbreite. Zur Berechnung des Mitteldrucks
und der daraus resultierenden Leistung des Wankelmotors ergeben sich folgende Formeln.
Vh=2*Vk*is, Vh der äquivalenter Hubraum, is= Anzahl der Scheiben,Vk = Kammervolumen, Gesamtkammervolumen Vkg = Vk*is.
Pe
= n * Vkg * Pm Hier kommt die gleiche Leistungsformel wie beim 2T-HKM zur Anwendung, da der Wankelmotor bei jeder Exzenterwellenumdrehung Leistung abgibt.
Pme=(2*pi*Me)/(Vh*i) = We/(Vh*i) ; i=0,5
Arbeitsspiele pro Umdrehung für das Viertaktverfahren, hierdurch erhalten wir dann wieder das Gesamt-Kammervolumen im Nenner. Rechnet man gleich mit Gesamtkammervolumen Vkg so erhält man Pme=(2*pi*Me)/(Vkg*i) hier
ist i gleich 1 zu setzen, wegen 1 Arbeitsspiel pro Exzenterwellenumdrehung. Im Endeffekt erhält man so das gleiche Ergebnis ohne den Umweg über Vh. Hintergrund, wie schon bekannt, der Wankelmotor hat keinen Leertakt
wie ein 4T-HKM. Schlußendlich ergeben sich die gleichen Formeln wie für den Zweitakter.
Me=(0,5*Vh*Pme)/(2*pi) = (Vkg*Pme)/(2 * pi) ; pi = Kreiszahl
Pe = effektive Leistung an der Exzenterwelle
We = Effektive Arbeit an der Exzenterwelle
Me= Effektvies Drehmoment
Pme = effektiver Mitteldruck in Pa
Vk Kammervolumen und Vkg Gesamtkammervolumen des Motors in m^3
Vh äquivalentes Hubvolumen um mit einen 4T-HKM vergleichbar zu sein.
n= Exzenterwellendrehzahl
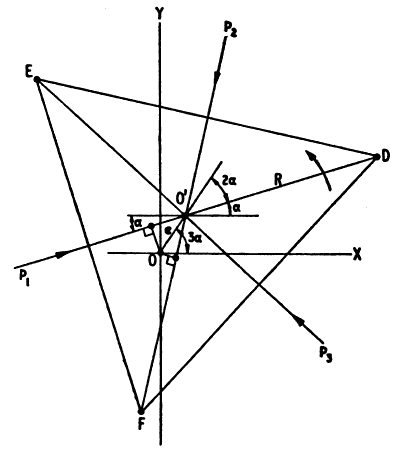
Man kann die ganze Sache auch grafisch ermitteln.
Wobei der resultierende Druck sich aus folgender Grafik berechnen lässt.
Das Drehmoment errechnet sich aus p1 mal m1 = e sin 2 alpha.
Wobei e die Exzentrizität ist.
p2m2= e sin (pi/3 - 2 alpha)
p3m3= e sin (2pi/3 - 2 alpha)
Der Druck ergibt sich aus folgender Beziehung:
T(alpha) = Ae[p1 sin 2 alpha + p2 sin (pi/3 - 2 alpha) - p3 sin (pi/3 + 2 alpha)]
A = die effektive Kolbenfläche
p1,2,3= der jeweilige Druck in der Kammer
m1,2,3= das resultierende Drehmoment
Me = FG . r = FG . e sin 2/3 alpha
© Grafik Wankelstiftung
|